В алгебре логики, термин "три палочки" означает использование символа "∴" для обозначения следствия или логического вывода. Этот символ, который состоит из трех вертикальных палочек, часто используется для выражения логической связи между предпосылками и заключением.
Понятие "три палочки" имеет свои основные определения. Во-первых, оно говорит о том, что если предпосылки истинны, то заключение также должно быть истинно. Это означает, что если мы имеем логическую связь между предпосылками и заключением, и если предпосылки верны, то мы можем сделать вывод о верности заключения.
Во-вторых, "три палочки" обозначает импликацию или условную конструкцию. Это означает, что мы говорим о том, что если предпосылки истинны, то заключение также будет истинно. В случае, если одна или обе предпосылки ложны, мы не можем делать каких-либо выводов о истинности заключения.
Термин "три палочки" в алгебре логики является важным понятием для понимания логического вывода и импликации. Он позволяет нам анализировать и оценивать связи между предпосылками и заключением и делать выводы о их истинности. Важно отметить, что "три палочки" применяется в различных областях, включая математику, философию и информатику.
Общие понятия в алгебре логики

Алгебра логики - это раздел математики, который изучает формальные правила и операции, которые могут быть применены к логическим выражениям. Она предоставляет инструменты для работы с различными видами символов и операций, которые могут быть использованы для анализа и манипулирования логическими утверждениями.
В алгебре логики существуют несколько основных понятий, которые важны для понимания и применения этой математической дисциплины:
- Логические операции: алгебра логики определяет несколько основных операций, таких как конъюнкция (И), дизъюнкция (ИЛИ), отрицание (НЕ) и импликация (ЕСЛИ... ТО).
- Логические переменные: это символы или выражения, которые представляют конкретные значения или пропозиции в логическом выражении. Логические переменные могут быть истинными (1) или ложными (0).
- Логические выражения: это комбинации логических переменных и операций, которые формируют утверждения или высказывания, которые могут быть верными или ложными.
- Таблицы истинности: это таблицы, которые показывают значения истинности логических выражений в зависимости от значений логических переменных. Таблицы истинности используются для анализа логических выражений и определения их истинности.
- Де Моргановы законы: это правила, которые позволяют выразить отрицание сложной логической операции через отрицание простых логических операций. Де Моргановы законы полезны при упрощении логических выражений.
Все эти понятия являются основными в алгебре логики и позволяют анализировать, манипулировать и решать задачи, связанные с логическими выражениями. Понимание этих понятий является важным для понимания и применения алгебры логики в разных областях, таких как математика, информатика и философия.
Логическая операция "три палочки"
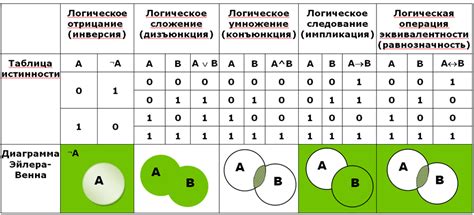
В алгебре логики существует ряд логических операций, одной из которых является операция "три палочки". Эта операция, также известная как сложение по модулю 2 или исключающее ИЛИ, обозначается символом "⊕".
| Аргумент 1 | Аргумент 2 | Результат |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Операция "три палочки" возвращает значение 1, если один из аргументов равен 0, и значение 0, если оба аргумента равны 1.
Также операция "три палочки" можно представить в виде таблицы истинности:
| Аргумент 1 | Аргумент 2 | Результат |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Операция "три палочки" имеет свойства коммутативности и ассоциативности.
Например, для двух аргументов A и B:
- (A⊕B) = (B⊕A)
- (A⊕B)⊕B = A
Операция "три палочки" может быть полезна при решении различных логических задач, таких как проверка четности числа или операции с битами. Она широко используется в различных областях, включая компьютерную науку и криптографию.
Символы и обозначения в алгебре логики
Алгебра логики - это отрасль математики, изучающая математические структуры и операции, связанные с логическими выражениями, значениями и их взаимосвязями.
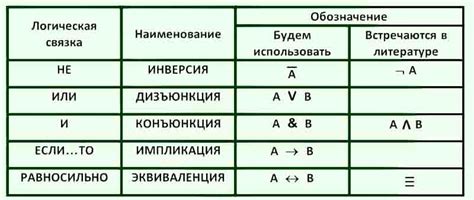
Одним из основных инструментов алгебры логики являются символы и обозначения, которые используются для представления и работы с логическими выражениями. Вот некоторые из наиболее распространенных символов и обозначений:
- Предикаты: Предикаты - это выражения, которые зависят от переменных и принимают значение "Истина" или "Ложь". Обычно они обозначаются буквами p, q, r и так далее.
- Конъюнкция (логическое умножение): Конъюнкция - это логическая операция, которая возвращает истинное значение только тогда, когда оба своих аргумента истинны. Она обозначается символом "∧".
- Дизъюнкция (логическое сложение): Дизъюнкция - это логическая операция, которая возвращает истинное значение, если хотя бы один из ее аргументов истинен. Она обозначается символом "∨".
- Импликация: Импликация - это логическая операция, которая говорит о связи между двумя высказываниями. Она обозначается символом "→".
- Инверсия (отрицание): Инверсия - это логическая операция, которая меняет истинность высказывания на противоположную. Она обозначается символом "¬".
В алгебре логики также используются таблицы истинности, которые позволяют определить истинность логического выражения в зависимости от значений его аргументов. Кроме того, для более сложных логических выражений могут применяться скобки и другие соглашения о приоритете операций.
Использование символов и обозначений в алгебре логики позволяет удобно и компактно записывать и работать с логическими выражениями, а также анализировать их и выводить логические заключения.
Определение "три палочки" в алгебре логики
Выражение "три палочки" в алгебре логики относится к понятию триади. Триада или "три палочки" - это система алгебраической символики, предложенная Чарльзом Сандерсом Пирсом в 1880-х годах.
Триада состоит из трех основных операций: конъюнкция (∧), дизъюнкция (∨) и отрицание (¬). Каждая из этих операций может принимать два аргумента и возвращать результирующее значение в виде истина (1) или ложь (0).
Конъюнкция (∧) представляет собой логическую операцию "И" и возвращает истину только в том случае, когда оба аргумента истинны.
Дизъюнкция (∨) представляет собой логическую операцию "ИЛИ" и возвращает истину, если хотя бы один из аргументов истинен.
Отрицание (¬) представляет собой логическую операцию "НЕ" и меняет истинность аргумента на противоположную: если аргумент истинен, то отрицание вернет ложь, и наоборот.
Триада включает также две дополнительные операции: импликация (→) и эквиваленция (↔). Импликация представляет собой логическую операцию "ЕСЛИ ..., ТО ..." и возвращает ложь только в случае, когда аргументы истины различны. Эквиваленция представляет собой логическую операцию "ЕСЛИ И ТОЛЬКО ЕСЛИ" и возвращает истину только в том случае, когда аргументы истины совпадают.
Триада является основой алгебры логики и используется для формализации и изучения логических высказываний, построения логических систем и решения логических задач.
Основные правила работы с "тремя палочками"
В алгебре логики термин "три палочки" обозначает логическую операцию "логическое или", которая также может быть обозначена символом "∨". Ниже приведены основные правила, с помощью которых можно работать с этой операцией.
- Свойство коммутативности: Для любых двух выражений A и B выполняется следующее правило: A ∨ B = B ∨ A. Это означает, что порядок операндов не важен.
- Свойство ассоциативности: Для любых трех выражений A, B и C выполняется следующее правило: (A ∨ B) ∨ C = A ∨ (B ∨ C). Это означает, что при наличии нескольких операций "три палочки" их можно группировать по своему усмотрению.
- Свойство дистрибутивности: Для любых трех выражений A, B и C выполняется следующее правило: A ∨ (B ∨ C) = (A ∨ B) ∨ (A ∨ C). Это означает, что операция "три палочки" можно распределить между скобками.
- Нейтральный элемент: Существует такое выражение X, что для любого выражения A выполняется следующее правило: A ∨ X = A. Выражение X называется нейтральным элементом относительно операции "три палочки".
- Абсорбционное правило: Для любых двух выражений A и B выполняется следующее правило: A ∨ (A ∨ B) = A. Иными словами, если выражение A совпадает с одним из операндов операции "три палочки", то его можно удалить из выражения.
С помощью этих правил можно упростить и анализировать различные выражения в алгебре логики, которые включают операцию "три палочки".
Операции со "тремя палочками"

В алгебре логики "три палочки" - это символичное обозначение операций, используемых для работы с высказываниями. Они позволяют строить сложные логические выражения на основе простых высказываний.
Основными операциями с "тремя палочками" являются:
- Конъюнкция (логическое "и"). Обозначается символом "∧". Она позволяет составлять новое высказывание, которое истинно только в том случае, когда оба составляющих его высказывания истинны.
- Дизъюнкция (логическое "или"). Обозначается символом "∨". Она позволяет составлять новое высказывание, которое истинно, если хотя бы одно из высказываний, входящих в него, истинно.
- Импликация (логическое "если...то"). Обозначается символом "→". Она позволяет составлять новое высказывание, которое истинно только в случае, когда первое высказывание ложно или второе высказывание истинно.
- Эквиваленция (логическое "тогда и только тогда"). Обозначается символом "↔". Она позволяет составлять новое высказывание, которое истинно только в том случае, когда оба составляющих его высказывания истинны или оба ложны.
- Отрицание (логическое "не"). Обозначается символом "¬". Она позволяет получить логическое отрицание высказывания, т.е. высказывание, противоположное исходному.
Таблицы истинности и правила преобразования при работе с "тремя палочками" позволяют оперировать и анализировать сложные логические выражения, включающие в себя одну или несколько из данных операций.
Используя "три палочки", мы можем строить логические цепочки рассуждений, выявлять логические ошибки, а также анализировать и делать выводы на основе логических закономерностей и связей между высказываниями.
Законы алгебры логики, связанные с "тремя палочками"
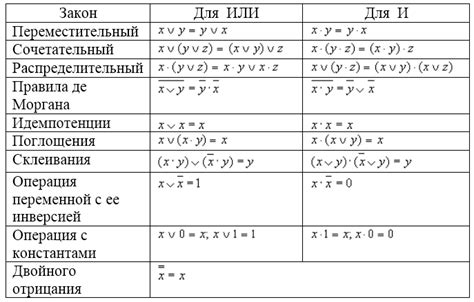
В алгебре логики, "три палочки" (¬) представляют отрицание или инверсию логического значения. Это унарный оператор, который изменяет значение выражения на противоположное. "Три палочки" можно использовать для выражения отрицания как отдельного составного выражения, так и для отрицания подвыражений в составных выражениях.
Законы алгебры логики, связанные с "тремя палочками":
- Закон двойного отрицания: двойное отрицание выражения равно самому выражению: ¬(¬A) = A
- Закон идемпотентности: двойное отрицание переменной равно самой переменной: ¬(¬A) = A
- Закон исключенного третьего: выражение A или ¬A принимает только одно из двух логических значений: A ∨ ¬A = 1
- Закон противоречия: выражение A и ¬A является противоречием и всегда ложно: A ∧ ¬A = 0
Также "три палочки" являются основным инструментом для построения и управления логическими операциями в алгебре логики, такими как конъюнкция (логическое И), дизъюнкция (логическое ИЛИ), импликация (логическое следствие) и эквивалентность (логическое равенство).
Применение "трех палочек" в различных областях
Понятие "трех палочек" или триады является одним из основных понятий в алгебре логики. Оно широко используется не только в математике, но и в других областях знания. Рассмотрим основные области, где применяются "три палочки".
1. Математика
В алгебре логики "трех палочек" используются для представления и анализа логических операций. Они позволяют описывать различные логические связи между высказываниями и применять операции конъюнкции, дизъюнкции и импликации.
2. Философия
В философии "три палочки" применяются для построения логических доводов и аргументации. Они помогают структурировать мысли и анализировать отношения между понятиями.
3. Информатика
В информатике "трех палочки" используются для построения логических цепочек и выражения условий в программах. Они позволяют контролировать ход выполнения программы в зависимости от различных условий.
4. Логика
Конечно, самая основная область применения "трех палочек" - это алгебра логики. Они используются для формализации и анализа различных логических отношений и операций, что делает их неотъемлемой частью логического мышления и рассуждений.
5. Математическая логика
В математической логике "три палочки" активно используются для представления и обработки формальных доказательств и выводов. Они позволяют строить корректные логические цепочки и аргументации.
6. Системы контроля версий
В современных системах контроля версий, таких как Git, "трех палочки" используются для обозначения различных состояний файлов или версий кода. Они позволяют удобно и наглядно отслеживать изменения и управлять версиями.
7. Дауншифтинг и менталитет
Для описания трех логических позиций, которые могут принимать люди в контексте работы и карьеры, такие фразы, как "белый воротничок", "серый воротничок" и "голубой воротничок" используются для различения найма и профессионального развития.
8. Маркетинг
В маркетинге "три палочки" применяются для классификации товаров или услуг в зависимости от их характеристик. Например, товары можно отнести к категориям "бытовая техника", "автомобили" и "одежда". Это позволяет ориентировать маркетинговые кампании на различные сегменты покупателей.
9. Психология и социология
В психологии и социологии "три палочки" используются для описания различных характеристик и типов личности или групп людей. Например, характеристики "экстраверт", "интроверт" и "амбиверт" отражают различные типы поведения и энергетику.
10. Лингвистика и логопедия
В лингвистике и логопедии "три палочки" используются для анализа звукового строя языка и выражения различных звуковых феноменов, таких как согласные, гласные и вокализация.
Таким образом, "трех палочки" или триады являются универсальным и мощным инструментом для анализа и структурирования различных понятий и отношений. Они находят применение во многих областях знания и позволяют более четко и ясно формулировать мысли и идеи.